S pomocí matemagických metod může vzniknout spoustu opravdu krásných věcí. Někdy taky ani ne moc krásných, ale to nevadí. Rozhodně mezi ty nejkrásnější patří fraktály, které mají mnoho využití, tedy pokud budeme mluvit o tvorbě sněhových vlček, nebo o využití buněčných automatů k simulacím vesmírných robotů. Nebo co.
Tuhle nedávno přišel Filipes a trochu verčil, že po útrapách objevili Rrrr a jsou z toho šťastní. A k tomu měli obrázek s Excelem. Pořád platí poučka, že se statistická věc nemá dělat v Excelu, protože na to máme speciální statistický software, takže tak asi. Ale myšlenka s R je moc krásná. Jde o to, že R je vál, který sice je GNU S, ale to už nikomu nic neřekne. Zkrátka a dobře je to svobodné prostředí pro výpočty snad libovolného druhu, s převážnou orientací na statistično a modelování. Výborně se hodí pro případy, kdy máme miliony dat a chceme je nějak zpracovat, ale SPSS chce nabíhat moc dlouho, nebo když je potřeba napsat si za okamžik jednoduchou LTSM neuronovou síť, ale všechny ostatní nástroje selžou. A hlavně, hlavně, všechno jsou to vektory a matice, podobně jako v MatLabu.
Dostupnost R zdarma je poněkud kryptická, protože se to blbě instaluje a ještě hůř se k tomu hledají návody a manuály, když se dá do Googlu jen jedno písmenko. Přestože jsou na oficiálním webu r-project.org k dispozici už hotové balíky pro různé platformy včetně Windows, nemá moc smysl pracovat mimo POSIXové prostředí, které citelně zrychluje práci. Jasně, člověk si musí trochu zvyknout na to, že se většinu času bude nacházet jen v terminálu a neuvidí obrázky přímo, ale zas to nabídne takovou míru automatizace, že pak celou práci zvládne udělat pomocí jednoho skriptu za pár minut.
Už nemám tušení, jak jsme na to celé vlastně přišli, ale už docela dlouho si chci nakreslit buddhabrot, nebo spíš nebulabrot, i když se t tak správně asi neříká. V tomhle R nemůže vyloženě pomoci kvůli poněkud problematické práci s barvami, ale jednoduchý základ, totiž krásně barevné fraktály v okolí Mandebrotovy množiny, dává na pána. Mandelbrotova množina, objevená Pierrem Fatouem, je sada čísel c ležících v komplexní rovině uvnitř kruhu o poloměru 2, resp. jsou to takové body, pro které je ve všech krocích n absolutní hodnota zn menší nebo rovna jak 2, a to při rekurzivní posloupnosti zn
$$ z_0\,=\,0\,,\,z_{n+1}\,=\,z_{n}^{2}+c. $$
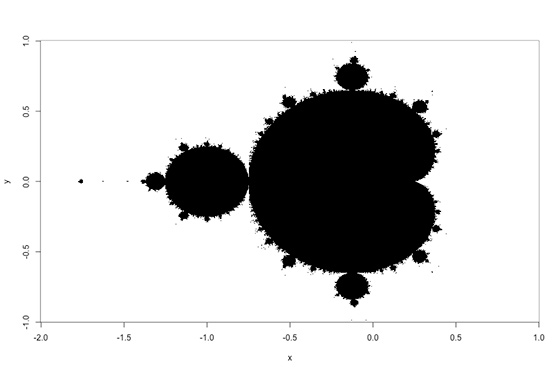
Po vykreslení na plátno, nebo prostě na nějaký graf, který zachycuje komplexní rovinu, vznikne podle uvedeného pravidla (abs. hodnota aktuálního zn je menší nebo rovna 2 = černá, jinak bílá) zhruba následující obrázek.
To ale není tak moc zajímavé, zajímavé jsou právě spíš všechny body mimo tuto množinu (tj. na jejím okraji, kousek za hranicí), které nesplňují podmínku a posloupnost utíká ven do nekonečna. Právě tyhle body začnou vytvářet oblasti, které při správném barevném zobrazení začnou vytvářet krásnou podívanou. No a abychom to vůbec mohli nakreslit, je potřeba někam bokem (třeba do k) počítat, kolikátá iterace (n) zrovna daným bodem prochází, nebo prostě rovnou vykreslit hodnotu n přímo do grafu komplexní roviny, kde už vstupuje do role případná barva.
Většinou není úplně v pořádku nastavit si taková počet barev, jako je zrovna maximální n, ačkoliv to pro určitý počet kroků může fungovat. Je dobré použít paletu spíš jako histogram a nechat výsledky rozpadnout do ekvivalenčních tříd, které budou mít přiřazenou nějakou konkrétní barvu. Vhodných barevných schémat pro Mandelbrotovu množinu se dá různě po Internetu najít značné množství, od nějakých ohnivých, šedivých, po žlutobílé, voňavé, s chutí malin… a dalších; asi zatím nejhezčí mi přijde kdesi objevený setík použitý v příkladech níže. Při kreslení buddhabrotů a nebulabrotů se pak využívá ještě natáčení v dalších rozměrech a práce s průhledností, která výsledku dodává říz. No ale pojďme si to celé nakreslit v R, protože proč ne, a protože je tu ještě jeden docela zajímavý aspekt, který je potřeba zohlednit.
Kde začít? Nejdřív je potřeba si promyslet, co je vlastně potřeba udělat a jak co vypadá. Základní tvar množiny, jak už byl zobrazen výše, se nachází v kruhu o poloměru 2, tedy budeme kreslit dvourozměrný graf tak, aby pokryl zmiňovanou oblast. Vhodné bude se tedy zamyslet, kde jsou levé a pravé okraje vodorovné (reálné) osy a kde budou horní a dolní okraje svislé (imaginární) osy. Příklady uvedené tady tak nějak počítají s tím, že si vždycky určíme střed grafu (X, Y) a odpovídající region, který byl později přepočítaný z průměru na poloměr (R), aby se dobře pracovalo s jinými ukázkami, které jsou online dohledatelné na mnoha místech. Celou množinu je proto na začátku vhodné situovat do středu (-0,5; 0), protože je značně posunutá k levé straně, a poloměr nastavit tak, aby zhruba pokryl celou oblast, takže od nějakých 1,5 do 2.
Další myšlenka je taková, že postupně budeme v každém kroku n procházet celou plochu obrázku od daných x-ových a y-ových souřadnic a zkoumat, zda je splněná daná podmínka, tedy že absolutní hodnota spočítaného z nepřesahuje 2. Ono je to z ale komplexní číslo, které je na začátku nulové, a později se mění pomocí c, které už obsahuje složky x a y tak, že x představuje reálnou část a y část imaginární. R umí pracovat s komplexními čísly celkem snadno, pro další zjednodušení je v příkladech použitá funkce outer(), která slučuje pole podle odpovídající funkce, takže můžeme vhodně inkrementovat její jednotlivé složky, následně y vynásobit imaginární jednotkou i a výsledek c jednoduše složit uvedenou funkcí +. Další použitá funkce je Mod(), která provádí výpočet velikosti komplexního čísla jako
$$Mod(z)\,=\,\sqrt{(x^2+y^2)}.$$
Snad není potřeba připomínat, že absolutní hodnota komplexního čísla představuje na zmíněném grafu vzdálenost tohoto čísla od počátku souřadnicového systému (0; 0i). Důležitou vlastností je tu ještě rozlišení, které vlastně říká, kolik kroků x a y bude použito na projití celého regionu. Pro optimální výsledky by hodnota mohla přibližně odpovídat rozměrům výsledného rastrového obrázku (co pixel, to jeden spočítaný bod — chce to zkoušet, kde to bude nejzajímavější).
#!/usr/local/bin/Rscript
# ^--- UNIXovy hashbang pro R pkg na macOS
# velikost obrazku (px)
px = 1280 + 90
py = 960 + 135
# PARAMETRY OBRAZKU
X = -0.5
Y = 0.0
R = 1.5
# rozliseni a pocet iteraci
resolution = 2000
n = 750
# vystupni adresar
dir = "vzorecek"
#-------------------------------------------------------------------------------
# nastaveni parametru do vypoctu
xcen = X
ycen = Y
regionsize = 2*R
#-------------------------------------------------------------------------------
# custom barevna skala
barvy <- c(
colorRampPalette(c("#e7f0fa", "#c9e2f6", "#95cbee",
"#0099dc", "#4ab04a", "#ffd73e"))(0.1 * n),
colorRampPalette(c("#eec73a", "#e29421", "#e29421",
"#f05336","#ce472e"), bias=2)(0.9 * n),
"black")
#-------------------------------------------------------------------------------
# snimek - pro pouziti ve smycce
filenamenum = 1000
png(paste(dir, "/", "frame-", filenamenum, ".png", sep="", collapse = NULL), px, py)
# region (1:1 pro w<h obrazky)
xregion = regionsize * 1
yregion = regionsize * py/px
# shodne rozliseni pro oba smery
nx = resolution * 1
ny = resolution * py/px
# stred regionu - nastaveni okoli
xmin = xcen - xregion/2
xmax = xcen + xregion/2
ymin = ycen - yregion/2
ymax = ycen + yregion/2
# souradnice (od-do po nx a ny krocich)
x <- seq(xmin, xmax, length.out=nx)
y <- seq(ymin, ymax, length.out=ny)
# inicializace komplexniho cisla C (x + yi)
c <- outer(x, y * 1i, FUN="+")
# inicializace vystupnich matic - Z (hodnota) a K (stupen) = 0.0
z <- matrix(0.0, nrow=length(x), ncol=length(y))
k <- matrix(0.0, nrow=length(x), ncol=length(y))
#-------------------------------------------------------------------------------
# VLASTNI VYPOCET
# vzoreckove dobrodruzstvi - pro kazde N
for (krok in 1:n) {
print(paste(krok, "(", filenamenum, ")", sep = "", collapse = NULL))
# iterace pro oba smery v ramci jednoho N
for (j in 1:ny) {
for (i in 1:nx) {
# overeni mezi komplexniho cisla
if (Mod(z[i, j]) < 2 && k[i, j] < n) {
# z1 = z0*z0 + c
z[i, j] <- z[i, j]^2 + c[i, j]
# stupen se zvysuje o 1
k[i, j] <- k[i, j] + 1
}
}
}
}
#-------------------------------------------------------------------------------
# zapis obrazku a zavreni bufferu (useRaster - starsi verze R jinak glitchuji)
image(x, y, k, col=barvy, useRaster = TRUE)
dev.off()
A teď to zajímavé. Tenhle příklad je sice přesně podle vzorečku a pracuje správně, ale tak nějak jsou v něm hned tři cykly, a tedy jeho výpočetní složitost je O(n3), což je na to, že prakticky nic rozumného nedělá, docela nesnesitelná palba. Vygenerovat celkem malý obrázek — 1280x720 pixelů (plus okraje grafu, které se dají zahodit později) — je i na docela našlapaných procesorech taková zátěž, že kdyby chtěl Filipes 8K video, asi by brzy vyhladověl čekáním.
R ale naštěstí chápe všechno jako vektory, nebo přímo jako matice, podobně jako MatLab. Ona je už i koncepce příkladu chápána jako práce na matici, tedy všechna z a z nich odpovídající barevné hodnoty k jsou definované na začátku jako matice a při každém kroku n se v nich prochází všechny jejich hodnoty. To ve výše uvedeném příkladu není úplně efektivní, když se použije for cyklus. Daleko snazší je pracovat s maticí jako s celkem, což je sice pro normálního člověka asi složitě představitelné, ale (moderní) počítače mají na rozdíl od človeků vektorové jednotky, jako je třeba AltiVEC, nebo prostě SIMD a SSE a AVX registry a takový ten chaos, který se s každou generací ještě rozšiřuje.
Myšlenka je tedy taková, že v každém kroku n zjistíme, které body ze všech v celé matici splňují požadovanou podmínku. K tomu je úžasná funkce which, protože pracuje s celým vektorem (maticí) najednou a vrací indexy původního pole, které splňují logickou podmínku. Pak už je velmi snadné prve zmiňované postupy aplikovat na celé matice z a k najednou a spočítat jejich nové hodnoty v jediném kroku. Tím se složitost papírově redukuje na O(n), ale ve skutečnosti je to ještě méně, protože jak which filtruje indexy přímo, jejich počet se vzrůstajícím n klesá, a tedy klesá i celková doba nutná pro zpracování kroku.
#!/usr/local/bin/Rscript
# ^--- UNIXovy hashbang pro R pkg na macOS
# velikost obrazku (px)
px = 1280 + 90
py = 960 + 135
# PARAMETRY OBRAZKU
X = -0.5
Y = 0.0
R = 1.5
# rozliseni a pocet iteraci
resolution = 2000
n = 750
# vystupni adresar
dir = "matice"
#-------------------------------------------------------------------------------
# nastaveni parametru do vypoctu
xcen = X
ycen = Y
regionsize = 2*R
#-------------------------------------------------------------------------------
# custom barevna skala
barvy <- c(
colorRampPalette(c("#e7f0fa", "#c9e2f6", "#95cbee",
"#0099dc", "#4ab04a", "#ffd73e"))(0.1 * n),
colorRampPalette(c("#eec73a", "#e29421", "#e29421",
"#f05336","#ce472e"), bias=2)(0.9 * n),
"black")
#-------------------------------------------------------------------------------
# snimek - pro pouziti ve smycce
filenamenum = 1000
png(paste(dir, "/", "frame-", filenamenum, ".png", sep="", collapse = NULL), px, py)
# region (1:1 pro w<h obrazky)
xregion = regionsize * 1
yregion = regionsize * py/px
# shodne rozliseni pro oba smery
nx = resolution * 1
ny = resolution * py/px
# stred regionu - nastaveni okoli
xmin = xcen - xregion/2
xmax = xcen + xregion/2
ymin = ycen - yregion/2
ymax = ycen + yregion/2
# souradnice (od-do po nx a ny krocich)
x <- seq(xmin, xmax, length.out=nx)
y <- seq(ymin, ymax, length.out=ny)
# inicializace komplexniho cisla C (x + yi)
c <- outer(x, y * 1i, FUN="+")
# inicializace vystupnich matic - Z (hodnota) a K (stupen) = 0.0
z <- matrix(0.0, nrow=length(x), ncol=length(y))
k <- matrix(0.0, nrow=length(x), ncol=length(y))
#-------------------------------------------------------------------------------
# efektivni SIMD/SSE vypocet
for (iter in 1:n) {
print(paste(iter, "(", filenamenum, ")", sep = "", collapse = NULL))
# velikost cisla
index <- which(Mod(z) < 2)
# matice [z1] = [z0*z0] + [c]
z[index] <- z[index]^2 + c[index]
# stupen
k[index] <- k[index] + 1
}
#-------------------------------------------------------------------------------
# zapis obrazku a zavreni bufferu (useRaster - starsi verze R jinak glitchuji)
image(x, y, k, col=barvy, useRaster = TRUE)
dev.off()
Nakonec tohle jednoduché zrychlení bude v řádech tisíců procent.
$ time ./single-loop.r
[1] "1(1000)"
...
[1] "750(1000)"
null device
1
real 15m47,862s
user 15m45,166s
sys 0m0,188s
#-----------------------
$ time ./single-vec.r
[1] "1(1000)"
...
[1] "750(1000)"
null device
1
real 1m17,911s
user 1m14,356s
sys 0m2,736s
To je taková věc k zamyšlení nad programováním, protože nikdo nechce čekat, když generuje 8K video, nebo nový wallpaper pro svůj notebook, případně matematickou kruto-cover fotku pro Facebook, aby ukázal, že je boss. Nebo nerd, záleží na úvaze. Ať už je to jakkoliv, možnost nastavit si parametry zobrazení hned od začátku dává možnost zkoumat tento překrásný fraktál do detailů na různých místech, z nichž jsou některé vybrané na této stránce a tady je jejich rekonstrukce.
Možná si někdo řekne, že přece není možný, aby jeden vzoreček dělal takový věci. Ale to je stejně jako v případě Eulerovy rovnosti — prostě Bůh je super, nenaděláš nic, výpočet nakonec vždycky zvítězí a my si budeme tato vítězství pamatovat už napořád. Tak snad jsou obrázky inspirativní a konečně říkají, že po dlouhém utrpení přichází jarní noci. Už byl čas. A bude zas. Juch.